If you’ve dipped your toes into machine learning, chances are you’ve already brushed against the sigmoid function. It's not loud or flashy. It's subtle—yet it plays a key role in turning complex models into ones that can learn, adapt, and generalize. The sigmoid function takes any real-valued number and squashes it neatly between 0 and 1. But there’s more going on under the hood. Let’s break it down—what it is, how it works, and why its derivative is so often mentioned alongside it.

What Is the Sigmoid Function and How Does It Work?

The sigmoid function is defined mathematically as:

σ(x)=11+e−x\sigma(x) = \frac{1}{1 + e^{-x}}σ(x)=1+e−x1​

Takes any real number and compresses it neatly between 0 and 1, making it ideal for interpreting outputs as probabilities. This is particularly useful in logistic regression and binary classification tasks, where model outputs reflect confidence or likelihood.

When passed through the sigmoid function:

• Large positive numbers approach 1, as e−xe^{-x}e−x becomes very small.
• Zero results in exactly 0.5, since e0=1e^{0} = 1e0=1.
• Large negative numbers approach 0, as e−xe^{-x}e−x grows large.

This creates its distinctive “S”-shaped curve.

The Derivative of the Sigmoid Function

If you’ve worked with training algorithms before, you’ll know that gradients—or derivatives—are everything. They tell us how to adjust our parameters to reduce the error. And luckily, the sigmoid function has a derivative that’s surprisingly tidy.

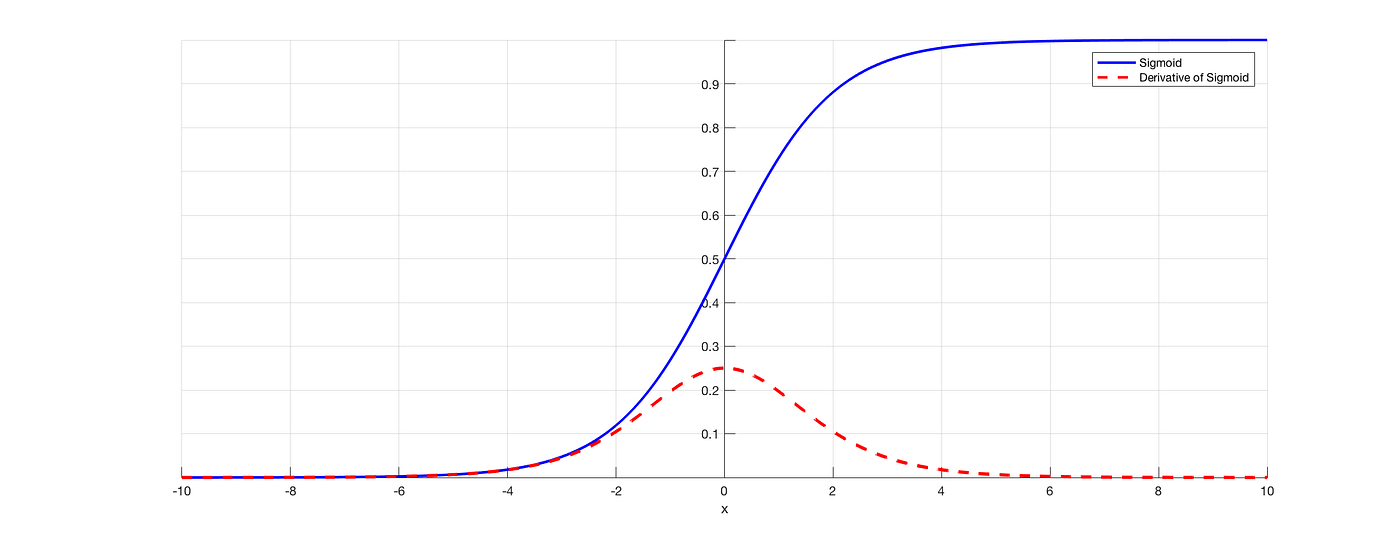
The derivative of σ(x) is:

    σ(x) * (1 - σ(x))

Yes, that’s it. The derivative of the sigmoid function depends directly on the output of the function itself. That means once you've calculated the output, you already have what you need to find the derivative. No extra exponential calculations needed.

Let’s put that into context. Imagine you’re training a neural network, and one of your hidden units outputs a value of 0.8. The gradient at that point would be:

    0.8 * (1 - 0.8) = 0.8 * 0.2 = 0.16

This tells us how sensitive the output is to changes in the input. In regions near 0 or 1, that product gets small, which is where things get tricky. Gradients close to zero can stall training, a phenomenon known as the vanishing gradient problem.

Still, the fact that the sigmoid derivative is bounded and relatively easy to compute makes it useful in simpler models where interpretability and ease of implementation matter more than raw speed.

Step-by-Step: How the Sigmoid Function Is Used in a Neural Network

Let’s walk through how the sigmoid function fits into a typical neural network, from input to output. We’ll use a basic example of binary classification.

Step 1: Initialize Weights and Biases

Every neuron starts with a set of initial weights and a bias value. These are usually set randomly at the beginning of training. They determine how much influence each input will have.

Step 2: Compute the Weighted Sum

When input values are fed into the network, each one gets multiplied by its corresponding weight. Then the bias is added. So the input to the sigmoid function looks like this:

    z = w₁x₁ + w₂x₂ + ... + wₙxₙ + b

This z is just a number, but it holds all the influence from the input layer.

Step 3: Apply the Sigmoid Function

Now, the output is calculated by plugging z into the sigmoid formula:

    σ(z) = 1 / (1 + e^(-z))

This converts the weighted sum into a probability-like value, neatly bounded between 0 and 1.

Step 4: Compare With the Target Output

The model's prediction is compared to the actual answer using a loss function, commonly binary cross-entropy when using sigmoid for classification. The goal is to reduce the difference between predicted and actual outcomes.

Step 5: Compute the Gradient

This is where the derivative comes in. During backpropagation, the derivative of the sigmoid function helps calculate how much each weight contributed to the error. Since we already know σ(z), we can quickly get:

    σ(z) * (1 - σ(z))

This gradient then flows backward through the network, guiding how the weights should change.

Step 6: Update the Weights

Using the calculated gradients, the weights and biases are adjusted (typically using gradient descent or some variant). The idea is to shift them in a direction that reduces the overall error.

And then—repeat. Dozens, hundreds, or even thousands of times. That’s training in a nutshell.

Where the Sigmoid Function Still Shines

While it’s true that newer activation functions like ReLU have largely taken over in deep learning architectures, the sigmoid function hasn’t been pushed aside completely. It still holds up well in models where interpretability is key. Logistic regression, for example, leans entirely on the sigmoid function. Why? Because its output can be read as a probability, which is exactly what’s needed in many real-world classification problems.

In shallow networks or binary classification setups, a sigmoid is often more than enough. It's straightforward, efficient, and easy to debug. When your goal is clarity over complexity, it's still a go-to option.

Final Thoughts

The sigmoid function might not be the flashiest tool in the machine learning toolkit, but it's one of the most practical. It's been around for decades, and despite the rise of deeper, more complex networks, it continues to earn its place, especially when clarity and simplicity are the priority. Its clean output, intuitive behavior, and easy-to-compute derivative make it a solid choice in many situations.

So the next time you're setting up a model and you see that familiar 1 / (1 + e^(-x)), know this: it’s not just a math formula. It’s a piece of machinery quietly doing its part to help your models learn and improve—one squashed number at a time. Stay tuned for more informative guides.